Four very long, current-carrying wires in the same plane intersect to form a square with side lengths of 45.0 cm, as shown in the figure blelow.
Joni Kenny
Answered question
2021-01-04
Four very long, current-carrying wires in the same plane intersect to form a square with side lengths of 45.0 cm, as shown in the figure below. The currents running through the wires are 8.0 A, 20.0 A, 10.0 A, and I.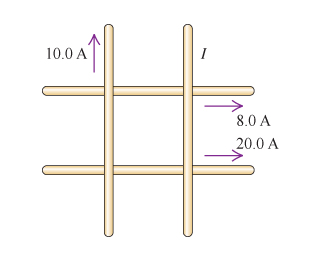
Part A
Find the current I that will make the magnetic field at the center of the square equal to zero.
Part B
What is the direction of the current I (up or down)?
Answer & Explanation
stuth1
Skilled2021-01-05Added 97 answers
Solution


Jeffrey Jordon
Expert2021-09-30Added 2605 answers
(A)
Consider the direction ‘into the page’ to be negative and the direction ‘out of the page’ to be positive.
The distance of each wire from the center of the square is half the side of the square. Thus, the distance R can be written as follows:
Here, a is the side of the square.
Substitute 45.0 cm for a in the above expression.
= 22.5 cm
Use right-hand thumb rule to find the direction of the magnetic field at the center of the square due to the current 8 A.
Place the thumb of right-hand in the rightward direction in which the current is flowing. Curl the fingers around the wire to see that the magnetic field at the center of the square to be into the page. According to the assumed sign convention, the direction of magnetic field in this case should be negative.
The magnetic field at the center due to 8.0 A wire can be written as follows:
Substitute 8.0 A for I in the above expression.
The magnetic field at the center due to 20.0 A wire can be written as follows:
Substitute 20.0 A for I in the above expression.
The magnetic field at the center due to 10.0 A wire can be written as follows:
Substitute 10.0 A for I in the above expression.
Now, the magnetic field at the center of the square is 0. Thus, the sum of all the magnetic fields must be equal to zero.
Here, B is the magnetic field in the 4th wire.
Substitute
The magnetic field due to the 4th wire is negative which means that the direction of magnetic field is ‘into the page’.
On comparing with the standard equation of magnetic field due to a current carrying wire, the current in the 4th wire is as follows:
Substitute
(B)
Due to wire with 8.0 A current, the magnetic field points ‘into the page’. This can be verified by right-hand thumb rule. Place the right hand in the direction of current 8.0 A. Curl the finger around it. The direction in which the fingers point at the center of the square gives the direction of the magnetic field due to this wire at the center. The direction comes out to be ‘into the page’.
Similarly, the direction of 20.0 A wire is ‘out of the page’.
Also, the direction of 10.0 A wire is ‘into the page’
Since, the magnetic fields due to 8.0 A and 10.0 A points ‘into the page’, they will add up.
This added quantity is still less than the magnetic field due to 20.0 A wire. Thus, there should be another 2.0 A current in the 4th wire, in a direction such that the remaining ‘out of the page’ magnetic field gets cancelled. For this, the magnetic field due to the 4th wire should point ‘into the page’.
Again, by right-hand thumb rule, curl the fingers around the 4th wire in such a way that the fingers goes into the page, the direction of the thumb will give the direction of the current in the 4th wire.
The direction of current comes out to be ‘downwards’.
New Questions in High School
At the beginning of an environmental study, ad forest covered an area of .Since then, this area has decreased by 4.25% each year.Let t be the number of years since the start of the study.Let y be the area that the forest covers in .
Write an exponential function showing relationship between y and t.Some friends tell you that they paid $25,000 down on a new house and are to pay $525 per month for 30 years. If interest is 7.8% compounded monthly, what was the selling price of the house? How much interest will they pay in 30 years?
t e^-4t sin3t
Find all whole number solutions of the congruence equation.
3x ≡ 8 mod 11Use a direct proof to show that the product of two rational numbers is rational.

Y=2(x-) (x+1)
what is vertex
axis of symmetry
x-intercept(s)
y-intercept
Stairs- Each step of a set of stairs has a tread depth of 11.5 inches and a riser height of 6.5 inches. What is the slope of the set of stairs?
A ball of mass 5 kg is attached to a string of length 10 cm, forming a pendulum. If the string is raised horizontally as shown and released from point A, then what is the v
assume that the random variable Xand Y have the joint pdf f(x,y)=1/2x^3
5=20 mod 4 true or false answer
5x−4y=
- −12
Pets Plus and Pet Planet are having a sale on the same aquarium. At Pets Plus the aquarium is on sale for 30% off the original price and at Pet Planet it is discounted by 25%.
Store Original Price
of Aquarium ($)Pets Plus 118 Pet Planet 110 If the sales tax rate is 8%, which store has the lower sale price?
, 1 of 1.Select ChoicePets PlusPet Planet has the lower sale price.
Part B
Fill in the blank question.
How much will you save by buying the aquarium at the store with the lower sale price? Round to the nearest cent.
$
Prove that if x is and irrational number and x>0 then route over x is also irrational
A small object has charge Q. Charge q is removed from it and placed on a second small object. The two objects are placed 1 m apart. For the force that each object exerts on the other to be a maximum. q should be: A. 2Q B. Q C. Q/2 D. Q/4 E. 0