Learn Derivatives with Practice Problems and Examples
Find the first derivative of the following exponential and logarithmic functions
A piece of wire 10 m long is cut into two pieces. one piece is bent into a square and the other is bent into a circle
How should the wire be cut so that the total area enclosed is (a) a maximum? (b) A minimum?
A piece of wire 10 m long is cut into two pieces. one piece is bent into a square and the other is bent into a circle
How should the wire be cut so that the total area enclosed is (a) a maximum? (b) A minimum?
Calculate the second derivative of the function
If f and g are the functions whose graphs are shown, let
u(x) = f(g(x)),
v(x) = g(f(x)), and w(x) = g(g(x)).
Find each derivative, if it exists. If it does not exist, explain why. (If an answer does not exist, enter DNE.)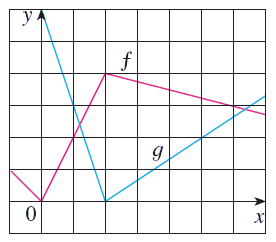
(a)
u'(1) =
It does exist.u'(1) does not exist because f '(1) does not exist. u'(1) does not exist because g'(1) does not exist.u'(1) does not exist because f '(3) does not exist.u'(1) does not exist because g'(2) does not exist.
(b)
v'(1) =
It does exist.v'(1) does not exist because f '(1) does not exist. v'(1) does not exist because g'(1) does not exist.v'(1) does not exist because f '(3) does not exist.v'(1) does not exist because g'(2) does not exist.
(c)
w'(1) =
It does exist.w'(1) does not exist because f '(1) does not exist. w'(1) does not exist because g'(1) does not exist.w'(1) does not exist because f '(3) does not exist.w'(1) does not exist because g'(2) does not exist.
If f and g are the functions whose graphs are shown, let
u(x) = f(g(x)),
v(x) = g(f(x)), and w(x) = g(g(x)).
Find each derivative, if it exists. If it does not exist, explain why. (If an answer does not exist, enter DNE.)
(a)
u'(1) =
It does exist.u'(1) does not exist because f '(1) does not exist. u'(1) does not exist because g'(1) does not exist.u'(1) does not exist because f '(3) does not exist.u'(1) does not exist because g'(2) does not exist.
(b)
v'(1) =
It does exist.v'(1) does not exist because f '(1) does not exist. v'(1) does not exist because g'(1) does not exist.v'(1) does not exist because f '(3) does not exist.v'(1) does not exist because g'(2) does not exist.
(c)
w'(1) =
It does exist.w'(1) does not exist because f '(1) does not exist. w'(1) does not exist because g'(1) does not exist.w'(1) does not exist because f '(3) does not exist.w'(1) does not exist because g'(2) does not exist.
Y=(4x+3)^4 (x+1)^-3 find the first and second derivatives
Y=(4x+3)^4 (x+1)^-3 find the first and second derivatives
Find the derivative of by first expanding the polynomials.
Enter the fully simplified expression for f (x) after expanding the polynomials
Enter the fully simplified expression for f (x) after expanding the polynomials
What is the derivative of ?
Do you use the product rule to multiply it out, or can youjust apply power rule to get: ?
Do you use the product rule to multiply it out, or can youjust apply power rule to get: ?
The graphs of f and g are shown. Let h(x) = f(g(x)) and s(x) = g(J(x)).
Find each derivative , if it exists. If the derivative ve does not exist, explain why.
Find h'( 1).
Find each derivative , if it exists. If the derivative ve does not exist, explain why.
Find h'( 1).
The graphs of f and g are shown. Let h(x) = f(g(x)) and s(x) = g(J(x)).
Find each derivative , if it exists. If the derivative ve does not exist, explain why.
Find s'(5).
Find each derivative , if it exists. If the derivative ve does not exist, explain why.
Find s'(5).
A cars velocity starting from rest is given by where v is measured in feet per second. Find the acceleration at the folowing times.
a. 5 seconds
b. 10 seconds
a. 5 seconds
b. 10 seconds