Expert Help with Non-Right Triangle Equations
One of the largest issues in ancient mathematics was accuracy-nobody had calculators that went out ten decimal places, and accuracy generally got worse as the numbers got larger. The famous Eratosthenes experiment. Given two similar triangles, one with small measurements that can be accurately determined, and the other with large measurements, but at least one is known with accuracy, can the other two measurements be deduced? Explain and give an example. The similarity of triangles gives rise to trigonometry.
How could we understand that the right triangles of trigonometry with a hypotenuse of measure 1 represent all possible right triangles? Ultimately, the similarity of triangles is the basis for proportions between sides of two triangles, and these proportions allow for the calculations of which we are speaking here. The similarity of triangles is the foundation of trigonometry.
One of the largest issues in ancient mathematics was accuracy-nobody had calculators that went out ten decimal places, and accuracy generally got worse as the numbers got larger. The famous Eratosthenes experiment. Given two similar triangles, one with small measurements that can be accurately determined, and the other with large measurements, but at least one is known with accuracy, can the other two measurements be deduced? Explain and give an example. The similarity of triangles gives rise to trigonometry.
How could we understand that the right triangles of trigonometry with a hypotenuse of measure 1 represent all possible right triangles? Ultimately, the similarity of triangles is the basis for proportions between sides of two triangles, and these proportions allow for the calculations of which we are speaking here. The similarity of triangles is the foundation of trigonometry.
Prove in detail the inequality of this formula:
Let x, y, z positive real number and
Let x, y, z positive real number and
What is the inradius of the octahedron with sidelength a?
1) Determine the height of one of two constituent square pyramids by considering a right triangle, using the fact that the height of the equilateral triangle is
2) Now cut the (solid) octahedron along 4 of these latter heights, i.e. across two non-adjacent vertices and two midpoints of parallel sides of the ''square base''. (Figure 1)
Consider the resultant rhombic polygon, whose sidelength is
So the question becomes: Is there a still simpler proof?

What is the inradius of the octahedron with sidelength a?
1) Determine the height of one of two constituent square pyramids by considering a right triangle, using the fact that the height of the equilateral triangle is
2) Now cut the (solid) octahedron along 4 of these latter heights, i.e. across two non-adjacent vertices and two midpoints of parallel sides of the ''square base''. (Figure 1)
Consider the resultant rhombic polygon, whose sidelength is
So the question becomes: Is there a still simpler proof?

I have a non-right-angled isosceles triangle with two longer sides, X, and a short base Y.
I know the length of the long sides, X.
I also know the acute, vertex angle opposite the base Y, lets
I know the length of the long sides, X.
I also know the acute, vertex angle opposite the base Y, lets
What is the value of x, if we have a triangle, where
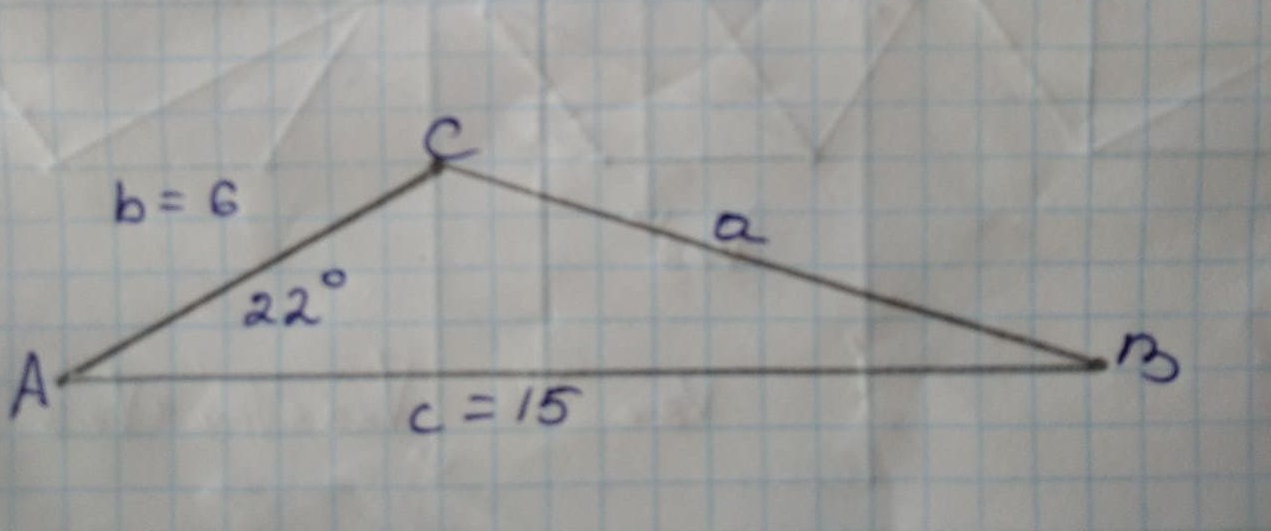
Help to solve the triangle ABC, given a=22, A=50, c=27.
Triangles ABC and DEF are right triangles, as shown.
Which ratios are equal to
Which ratios are equal to
Solve each of the following triangles. If there are two triangles, solve both. Round angle measurements to one
decimal place and side lengths to two decimal places.
a=
y=
c=
a=
y=
c=
Triangles ABC and DEF are similar triangles. Use this fact to solve the exercise. Round to the nearest tenth.
Find the perimeter of triangle ABC.

Find the perimeter of triangle ABC.

A pole has two wires attached to it, one on each side, forming two right triangles as shown.


triangle ABC is a right triangle with its right angle at C. The bisector of angle B intersects AC at D. The bisector of the exterior angle at B intersects AC at E. If BD= 15 and BE=20, what are the lengths of triangle ABC?
Use the Law of Cosines to solve the triangles. Round lengths to the nearest tenth and angle measures to the nearest degree.
Use the Law of Cosines to solve the triangles. Round lengths to the nearest tenth and angle measures to the
nearest degree. PLEASE solve both of these triangles. Thank you!