Important questions of Geometry for SSC CGL Tier I In my previous session, I have discussed some concepts related to triangles. Today I will discuss s

Important Examples

Example1: ABCD  is a cyclic quadrilateral. AB and CD are produced to meet P. If angle ADC = ${70}^o$and $\mathrm{\angle }$$DAB={60}^o$, then what will be angle $PBC+\mathrm{\angle }PCB$?

Solution: First step: Make an appropriate figure using statements provided in  questions.

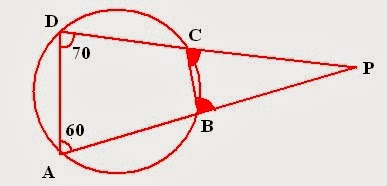
• Cyclic quadrilateral has all its vertices on circle and sum of all angles is ${360}^{\circ }$.
• Sum of opposite angles = ${180}^{\circ }$.
• External angle = Opposite internal angle.  

Therefore, $\mathrm{\angle }$ $PBC={70}^o$
$\mathrm{\angle }$$PCB={60}^o$

So, $PBC+PCB={130}^0$

See its very simple question, if you know the properties of geometry. Let's try more examples

Example2: ABCD is a parallelogram and P is any point within it. If area of parallelogram is 20 units, then what will be the sum of areas of triangle PAB and PCD?

Solution: According to the question, figure will be as follows:

Properties for this question:

• Area of parallelogram = Base times Height.
• Area of triangle = 1/2 Base times altitude.

Given that: Area of parallelogram = 20
i.e. Base times Height = 20
 $\Rightarrow b\times h=20$

To find =  Area of ( PAB +PCD)
$\Rightarrow (1/2)b\times (PY)+(1/2)b\times (PX)$ ( See Figure)

$\Rightarrow 1/2b(PX+PY)$


$\Rightarrow 1/2bh$
⇒(1/2) $\times$ 20
$\Rightarrow 10units$.

Example3: ABCD is a cyclic trapezium with AB parallel DC and AB diameter of circle. If $\mathrm{\angle }$$CAB={30}^o$, then $\mathrm{\angle }ADC$ will be?

Solution: According to ques, figure will be as follows:

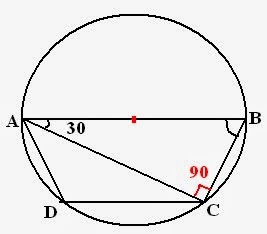
• Angle subtended by diameter is always ${90}^{\circ }$.
• Sum of angles of triangle = ${180}^o.$
• Sum of opposite angles = ${180}^o$

$\mathrm{\angle }$ $ACB={90}^o$
$\mathrm{\angle }$ $BAC={30}^o$

Therefore, 


$\mathrm{\angle }$ $ABC={60}^o$
angle $ABC+\mathrm{\angle }$ $ADC={180}^o\Rightarrow {60}^o+ADC={180}^o$⇒ $\mathrm{\angle }$ $ADC={120}^o$
Example4: Two side of plot measures 30m and 22m and angle between them is ${90}^o$. The other two sides measures 24m and the three remaining angles are not right angles. Find the area of plot.
Solution: Figure becomes: Center point of BD = O

ABD is a right angle triangle, therefore, Pythagoras theorem followed.
$(BD{)}^2=(AB{)}^2+(AD{)}^2\Rightarrow BD=40$
Given that, $BC=CD$ Therefore, line drawn from C to BD given right angles Also, this will lead to DO = BO
So, $DO=BO=20$
Similarly, using Pythagoras theorem, $OC=15m$

Now, Area of triangles $(ABD+BOC+COD)\Rightarrow 1/2(24\times 32)+2((1/2)20\times 15)\Rightarrow 684$ $m^2$