a) In 5 years, twice a puppy's current age will be equal to or greater than 15. What is the least integer that satisfies the inequality 2x+5 ge 15?
Haley Madden
Answered question
2022-07-24
b) To the nearest square meter, what is the area of the figure below?
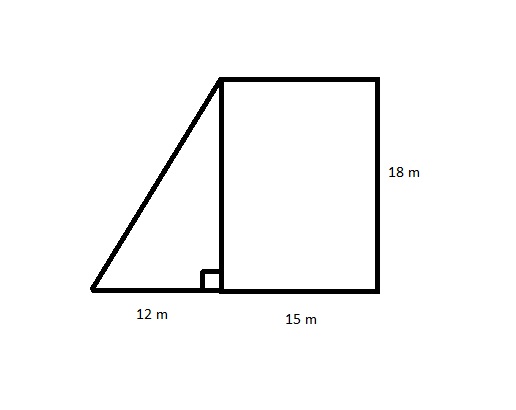
c) The Philippine Trench in the Pacific Ocean is 10.05 kilometers deep. The Brazil Basin in the Atlantic Ocean is 6.12 kilimeters deep. To the nearest hundredth of a kilometer, how many kilometers deeper than the Brazil Basin is the Philippine Trench?
d) A supermarket is having a sale on canned foods. The sale includes 12 cans of soup for . What is the unit price per can of soup to the nearest cent?
Answer & Explanation
Cheyanne Charles
Beginner2022-07-25Added 13 answers
a) The leart integer canbe find as undear
Step 2
b) The area of the fig
The area of
triangle
Now area of rectangle
Urijah Estes
Beginner2022-07-26Added 5 answers
c) Solve: The philippine trench = 10.05 km
The Brazil basin = 6.12 km
Therefore the philippine trench is deeper then Brasil basin by
i.e 3.93 km Answer
Step 2
Solve:
Since:
Now: 12 cans of cost =1065
New Questions in Pre-Algebra
Which expression has both 8 and n as factors???
One number is 2 more than 3 times another. Their sum is 22. Find the numbers
8, 14
5, 17
2, 20
4, 18
10, 12Perform the indicated operation and simplify the result. Leave your answer in factored form
An ordered pair set is referred to as a ___?
Please, can u convert 3.16 (6 repeating) to fraction.
Write an algebraic expression for the statement '6 less than the quotient of x divided by 3 equals 2'.
A)
B)
C) 3x−6=2
D)Find: .
Multiplication equals.
Solve: (128÷32)÷(−4)=
A) -1
B) 2
C) -4
D) -3What is converted into a fraction?
The mixed fraction representation of 7/3 is...
How to write the algebraic expression given: the quotient of 5 plus d and 12 minus w?
Express 200+30+5+4100+71000 as a decimal number and find its hundredths digit.
A)235.47,7
B)235.047,4
C)235.47,4
D)234.057,7Find four equivalent fractions of the given fraction:
How to find the greatest common factor of ?