Basic facts and techniques of Boats and Streams of Quantitative Aptitude Boats and Streams is a part of the Quantitative aptitude section. This is jus

Basic Concept

If direction of boat is same as direction of the stream, then it is known as DOWNSTREAM and if directions are opposite, then it is known as UPSTREAM. Following figure is representing the same: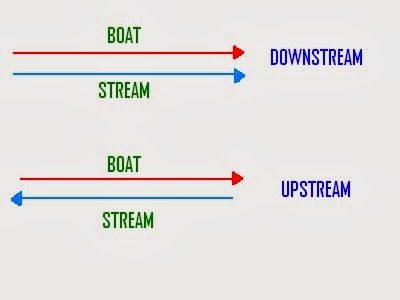



For example, a boat is said to be moving downstream if it is moving with the stream or upstream if it is moving against the stream.

Downstream Speed and Upstream Speed

When going downstream, the stream and boat speeds will be summed to determine the downstream speed because the direction is the same.
If Speed of boat in still water $=ukm/hrSpeedofstream=vkm/hr$, then
Downstream Speed $=(u+v)km/hr$
Similarly, if I talk about upstream speed, as the direction of boat and stream is opposite, speed of both will be subtracted.
i.e. Upstream Speed $=(u-v)km/hr$
Study the following figure, notice the directions and try to remember this i.e. If directions are same then speeds will be added and If directions are opposite then speeds will be subtracted

Speeds of Boat and Stream if Downstream and Upstream Speeds are given

Speed of Boat $=1/2(\text{Downstream Speed}+\text{Upstream Speed})$
Speed of Stream $=1/2(\text{Downstream Speed}-\text{Upstream Speed})$

Problems with Solution

Example1: In still water, a boat can move at a speed of 5 km/h, while a stream moves at 1 km/h. Calculate the downstream and upstream speeds.
Solution: Given that, $u=5$ km/hr
$v=1$ km/hr
Downstream speed $=u+vkm/hr\Rightarrow 5+1=6km/hr$
Upstream speed $=u-vkm/hr\Rightarrow 5-1=4km/hr$
Example 2: A man takes 3 hours to row a boat 15km downstream of river and 2 hours 30 min to cover a distance of 5 km upstream. Find speed of river or stream.
Solution: From downstream and upstream speeds, we must determine the stream's speed. See my calculation here:
As You know, Speed = Distance/ Time
So, Downstream Speed $=(15)/3=5km/hr\text{Upstream Speed}=5/2.5=2km/hr$
Now, As i have discussed, Speed of stream $=1/2(\text{Downstream Speed}-\text{Upstream Speed})$
$\Rightarrow \text{Speed of stream}=1/2(5-2)\Rightarrow 3/2=1.5km/hr$
Example 3: A man can row 7km/hr in still water. If in a river running at 2 km/hr, it takes him 50 minutes to row to his place and back, how far off is the place? *Important Question*
Solution: Given, $u=7km/hrv=2km/hr$ From u and v , we can calculate Downstream speed and upstream speed.
Downstream Speed $=(u+v)=7+2=9$ km/hr Upstream Speed $=(u-v)=7-2=5$ km/hr
Now, we need to find DISTANCE and time is given,
$Time=Distance/Speed$
Let required distance $=x$ km
Time taken in downstream + Time taken in upstream $=\text{Total Time}\Rightarrow (x/9)+(x/5)=(50)(60)$........................ $50minutes=(50)(60)hrs$
$\Rightarrow \text{Calculating the above equation}:x=2.68km$