Angle theorems Uncovered: Discover the Secrets with Plainmath's Expert Help

Finding the side and angle of a triangle.
The following diagram shows the triangle ABC.

$AB=6cm,BC=10cm,\text{and}A\stackrel{^<!--\; ^\; -->}{B}C={100}^{\circ <!--\; \circ \; -->}$

Angle bisector theorem for computing an angle
Trianlge ABC has $AB=33,AC=88,BC=77.$. Point D lies on BC with $BD=21.$. Compute $\mathrm{\angle <!--\; \angle \; -->}BAD.$.

Square of the angle bisector in a triangle.
Prove that the square of the length, 'd' of the angle bisector AL of $\mathrm{\angle <!--\; \angle \; -->}A$ meeting BC at L in a $\mathrm{\Delta <!--\; \Delta \; -->}ABC$ is $bc(1-<!--\; -\; -->{\left(\frac{a}{b+c}\right)}^2).$

Find angle of isosceles triangle
Let ABC an isosceles triangle ($AB=AC$) and the bisector from B intersects AC at D such that $AD+BD=BC$. Find the angle A.

In triangle ABC, $AB=84,BC=112$, and $AC=98$. Angle B is bisected by line segment BE, with point E on AC. Angles ABE and CBE are similarly bisected by line segments BD and BF, respectively. What is the length of FC?

An Olympiad Geometry problem with incenter configurations.
Let the inscribed circle of triangle ABC touches side BC at D ,side CA at E and side AB at F. Let G be the foot of the perpendicular from D to EF. Show that $\frac{FG}{EG}=\frac{BF}{CE}$.
So this problem is equivalent to proving similarity between $\mathrm{\Delta <!--\; \Delta \; -->}BFG$ and $\mathrm{\Delta <!--\; \Delta \; -->}CEG$.
I was able to prove that $\mathrm{\angle <!--\; \angle \; -->}GFB$= $\mathrm{\angle <!--\; \angle \; -->}GEC$ but after that, I hit a dead end. I found the point G pretty annoying as I couldn't apply any circle theorems to it.

Formal definition of trigonometric functions
I want to define trigonometric function (say sine) formally with the definition that the sine of an angle is the ratio of the length of the opposite side to the length of the hypotenuse. But there is a problem with defining an angle (and the measure of an angle) without knowing trigonometric functions. Some people say that the measure of an angle is the ratio of the lenth of the arc to the lenght of the radius. But I don't know how to define an arc without trigonometric functions.
The solution may be to define sine and cosine with power series. I know this approach and it's fine, but I'm interested in classical definition.
So I came up with my own idea. Let $x\in <!--\; \in \; -->(0,90)$ and let P be a model of Hilbert's plane euclidian geometry, $\mathrm{\mu <!--\; \mu \; -->}$ is segments measure, $\mathrm{\nu <!--\; \nu \; -->}$ is angles measure such that the emasure of the right angle is 90, and $\mathrm{△<!--\; △\; -->}abc$ is a right triangle in which $\mathrm{\nu <!--\; \nu \; -->}(\mathrm{\angle <!--\; \angle \; -->}abc)=x$. Then $\sin <!--\; \; -->x=\frac{\mathrm{\mu <!--\; \mu \; -->}(ac)}{\mathrm{\mu <!--\; \mu \; -->}(ab)}$.
This definition requires proving many theorems (for instance existance of measures and triangle with given angles) and you have to prove that the definition doesn't depnd on the choice of the model, choice of the segments measure and choice of the right triangle.
The question is: Can we define angles and sine without referring to Hilbert' theory? Maybe it's possible to define measure of angles in euclidian model ${\mathbb{R}}^2$. I think the key part of the definition must be additivity of the measure, as it is in Hilbert's theory.

Proof with congruence of angles
Suppose we have angle PQR with P, Q, and R non-collinear, and ray QS distinct from ray QR such that angle PQS is congruent to angle PQR. Prove that if angle PQT is congruent to angle PQR, then either ray $QT=$ ray QR or ray $QT=$ ray QS.

Prove the sum of intern angles of a quadrilateral is equal to ${360}^{\circ <!--\; \circ \; -->}$
You can use the information: theorem "The sum of all angles in a triangle is equal to $180º$" to prove the sum of all angles in a quadrilateral is ${360}^{\circ <!--\; \circ \; -->}$.

Let BD bisect $\mathrm{\angle <!--\; \angle \; -->}ABC$ in $\mathrm{\Delta <!--\; \Delta \; -->}ABC$. Given $\mathrm{\angle <!--\; \angle \; -->}ABC=60$ degrees and $AB=BC+CD$, find $\mathrm{\angle <!--\; \angle \; -->}BAC$

Find angles in a right triangle if $\tan <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}=\frac{3}{4}$, where $\mathrm{\theta <!--\; \theta \; -->}$ is the angle between medians
Find angles in right triangle if it is known that $\tan <!--\; \; -->\mathrm{\theta <!--\; \theta \; -->}=\frac{3}{4}$, where $\mathrm{\theta <!--\; \theta \; -->}$ is the angle between catheti medians.

Find the measure of an angle
Let ABC a triangle with the measure of angle B equal to 56 degrees and the measure of angle C equal to 36 degrees. P is a point on the side AB, and Q on the side AC so$BP=CQ=1$. Let M be the middle of the side BC and $BM=MC=5$. Also, be N the middle of the PQ side. Find out the BMN angle measurement.
Given that there are given lengths of sides, I try to use the sine theorem in the triangles BPM, respectively CQM. Then I used the formula $\sin <!--\; \; -->(a)+\sin <!--\; \; -->(b)=2\sin <!--\; \; -->((a+b)/2)\cos <!--\; \; -->((a-<!--\; -\; -->b)/2)$ hoping to get some measure of that angle. Can you give me a hint, please?

There are circle with radius R1 and circle with radius R2. We also know the distance between A and O and that angle $AOB=\mathrm{\varphi <!--\; \varphi \; -->}$. The aim is to calculate distance between B and C.

True or false? Any triangle we can $h_A^2+h_B^2\ge <!--\; \ge \; -->2h_C^2$, where $h_A,h_B,h_C$ are lengths of the heights from vertices A, B and C
Let $\mathrm{△<!--\; △\; -->}ABC$ any triangle and the lengths of the heights from vertices A, B and C are, respectively, $h_A$, $h_B$, $h_C$. Then how should we prove that, $h_A^2+h_B^2\ge <!--\; \ge \; -->2h_C^2,h_C^2+h_A^2\ge <!--\; \ge \; -->2h_B^{2}and{h}_B^2+h_C^2\ge <!--\; \ge \; -->2h_A^2$

Solving a triangle, given two sides and the measure of the included angle
Let say you have a triangle
$\mathrm{\angle <!--\; \angle \; -->}A={41}^{\circ <!--\; \circ \; -->}$, side $b=3.41$ and $c=5.83$
Can you use pythagoras theorem to find the side a? and how can you find Angle B and C

Let ABC be a triangle and $\mathrm{\Omega <!--\; \Omega \; -->}$ be its circumcircle, the internal bisectors of angles A, B, C intersect $\mathrm{\Omega <!--\; \Omega \; -->}$ at $A_1,B_1,C_1$. The internal bisectors of $A_1,B_1,C_1$ intersect Omega $A_2,B_2,C_2$. If the smallest angle of $\mathrm{△<!--\; △\; -->}ABC$ is 40 degrees, find the smallest angle of $\mathrm{△<!--\; △\; -->}{A}_2{B}_2{C}_2$.

Solve a triangle given the two angles in which a median split a vertex angle
Given the two angles ${\mathrm{\alpha <!--\; \alpha \; -->}}_1$ and ${\mathrm{\alpha <!--\; \alpha \; -->}}_2$ in which a vertex angle of a triangle is split by the related median m, find the remaining angles of the triangle $\mathrm{\beta <!--\; \beta \; -->}$ and $\mathrm{\gamma <!--\; \gamma \; -->}$.

Triangles : isoceles and angles inside with other triangle
We have one main isoceles and another one inside of it. I have attached here a diagram, and we wish to find the angle in red:

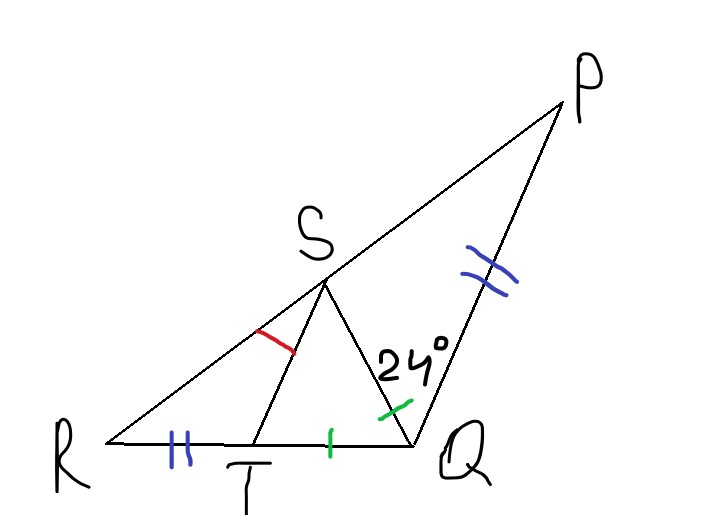
The labels blue means : lengths $PQ=QR$ The label green means : lengths $QS=QT$. The given angle $PQS=24$ (deg)
We wish to find angle in red, angle RST.