(a) Find the point at which the given lines intersect. r = 2, 3, 0 + t 3, −3, 2 r = 5, 0, 2 + s −3, 3, 0 (x, y, z) = (b) Find an equation of the plane that contains these lines.

Question

(a)  Find the point at which the given lines intersect.           r     =                                              2, 3, 0                                               +     t                                         3, −3, 2                                                    r     =                                              5, 0, 2                                               +     s                                         −3, 3, 0                                                  (x, y, z) = 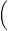                                             (b)  Find an equation of the plane that contains these lines.

Jeffrey Jordon · Accepted Answer

Set the two r vectors equal to each other. r=(2,3,0)+t(3,−3,3)=(2+3t,3−3t,3t) r=(5,0,3)+s(−3,3,0)=(5−3s,3s,3) 2+3t=5−3s 3−3t=3s 3t=3. Then it can be easily verified that t=1 and s=0 (divide both sides of the last equation by 3 and substitute the result into any of the two above it). Then this immediately tells us that (2+3t,3−3t,3t)=(5,0,3)=(5−3s,3s,3) is the point of intersection. b) Now, the normal vector of the plane is perpendicular to the directional vectors of both of the lines contained in the plane. Take the cross product of the two directional vectors to obtain this normal vector: &amp;lt;3,−3,3&amp;gt;×&amp;lt;−3,3,0&amp;gt;=&amp;lt;−9,−9,0&amp;gt;. Now, any nonzero scalar multiple of this normal vector is also a normal vector. Thus, &amp;lt;1,1,0&amp;gt; is a normal vector. With the normal vector and a point on the plane, such as the point of intersection, (5,0,3), we can write the equation of the plane containing the two given lines.  1(x−5)+1(y)+0(z−3)=0, which simplifies to x−5+y=0, or x+y=5.

(a) Find the point at which the given lines intersect. r = 2, 3, 0 + t 3, −3, 2 r = 5, 0, 2 + s −3, 3, 0 (x, y, z) = (b) Find an equation of the plane that contains these lines.

Answered question

Answer & Explanation

New Questions in Linear algebra