Be Pro in T-Statistic in No Time: Tips & Tricks

What is the $N$ in statistics?

Cece Adonai2022-12-11

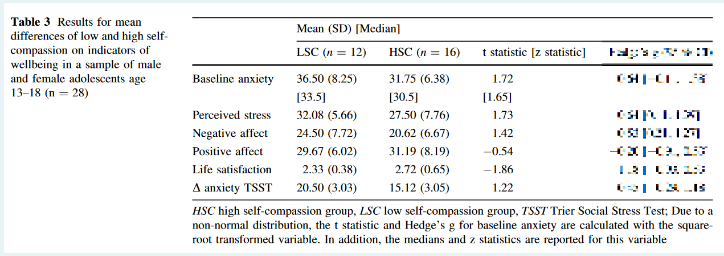
Which of the following statements is correct?

a.) With a larger sample, the mean differences examined here would increase (all other parameters remaining the same).

b.) If the standard deviations of the variable "Δ anxiety TSST" in both groups were smaller than those reported here, the t-value for the mean comparison of these variables would be larger (all other parameters being equal).

c) If, in addition to male and female adolescents, adolescents of diverse genders had also been interviewed, the t-test would no longer have been applicable. i

.e.) If it turned out that some questionnaires were incorrectly scored and the mean values for perceived stress in the group of high self-compassion were greater than 27.50, this would increase the t-value for the comparison of means (all other parameters being equal ). e.

d) To compare negative and positive affect within the group of people with low self-compassion, a one-sample t-test would be used.

Will Osborn 2022-11-24

When we take $X_{1}, . . ., X_{n}$ from $F (x)$ . Then the ranks are $X_{(1)} < . . . < X_{(n)}$ and lets take the test-statistic,
$\begin{aligned} t_{0} (X_{1}, . . ., X_{n}) = \sum_{i = 1}^{n} X_{(i)} \end{aligned}$
If we look at $t (- X_{1}, . . ., - X_{n})$ to see if $t (- X_{1}, . . ., - X_{n}) \overset{?}{=} - t (X_{1}, . . ., X_{n})$ , does the rank change?
For example is then $- X_{1}, . . ., - X_{n}$ correspond to $X_{(1)} < . . . < X_{(n)}$ ?

Aleah Avery 2022-11-23

Let $X_{1}, X_{2}, . . ., X_{n}$ be a random sample from a $N (θ_{1}, θ_{2})$ distribution. Find the uniformly minimum variance unbiased estimator of $3 {θ_{2}}^{2}$ .

Lorena Becker 2022-11-22

Consider a random sample of size n $n$ that follows a density probability function given by:
$f (x, θ) = \frac{1}{θ} x^{- \frac{θ + 1}{θ}} 1_{(1, + \infty)}, θ > 0$
where $θ$ is unknown.

jorgejasso85xvx 2022-11-20

Let $X_{1}, \dots, X_{n}$ be independent random variables with densities:
$f_{X_{k}} (x ∣ θ) = {\begin{cases} e^{k θ - x} & x \geq k θ \\ 0 & otherwise \end{cases}$
Find the pmf for $T = min_{k} (\frac{X_{k}}{k})$ .

Nola Aguilar 2022-11-20

Show that $\frac{1}{n} (\sum_{i = 1}^{n} \log \frac{1}{1 - X_{i}})^{3}$ is a sufficient statistic for $β$ in a Beta $(α, β)$ density

gfresh86iop 2022-11-19

Assume we have $Y_{1}, . . ., Y_{n}$ iid sample from the uniform distribution $U (0, θ)$ . Assume $T (Y_{1}, . . ., Y_{n}) = M i n_{1 <= i <= n} (Y_{i})$

reevelingw97 2022-11-18

Let $T$ be a complete suﬃcient real-valued statistic for the parameter $θ$ and $S$ be another real-valued statistic whose distribution function $F$ does not depend on the parameter $θ$ . Show that $P (S \leq s ∣ T) - F (s)$ equals zero almost surely under each $P_{θ}$ and for each real $s$ . Conclude from this that $S$ and $T$ are independent.

pin1ta4r3k7b 2022-11-17

Why would $T = X Y + Z$ not be a sufficient statistic for $X, Y, Z \sim_{i . i . d} B e r n (p)$

vidamuhae 2022-11-16

$f_{θ} (x)$ , then $T$ is sufficient for $θ$ if and only if nonnegative functions $g$ and $h$ can be found such that
$f_{θ} = h (x) g_{θ} (T (x))$

Alberto Calhoun 2022-11-08

Let $X_{1}, \dots, X_{n}$ be a random sample with the pdf
$f_{X_{i}} (x | θ) = {\begin{cases} e^{i θ - x}, & x \geq i θ \\ 0, & x < i θ \end{cases}$
Show that $T = min_{i} \frac{X_{i}}{i}$ is a sufficient statistic for $θ$ .

Aliyah Thompson 2022-11-08

Suppose ${X_{i} : i = 1, \dots, n}$ follows the parametric family of distribution $f (x_{1}, \dots, x_{n} | θ)$ .

Cael Dickerson 2022-11-07

Let $(X, M)$ , $(Y, N)$ and $(Z, O)$ be measurable spaces, and let $f : X \to Y$ and $g : Y \to Z$ be measurable functions. Then $σ (g \circ f) = σ (f)$ if and only if $g$ is bijective, where $σ (g \circ f) = (g \circ f)^{- 1} (O) = f^{- 1} (g^{- 1} (O))$ and $σ (f) = f^{- 1} (N)$ .

kemecryncqe9 2022-11-07

Suppose under the null hypothesis, the density of a test statistic $T$ is $f_{H_{0}} (t) = 2 t I (t \in [0, 1])$ , and under the alternate, the test statistic $T$ is $f_{H_{a}} (t) = 2 (1 - t) I (t \in [0, 1])$ .
Suppose $H_{0}$ is true (so $T$ has density $f_{H_{0}} (t)$ .) What is the probability that $f_{H_{0}} (T) / f_{H_{a}} (T) \leq 0.5$ ?

Aleah Avery 2022-11-06

Let $θ^{'}$ , $θ \in Θ$ such that $θ^{'} \neq θ$ .Prove that $T$ is a sufficient statistic if and only if
$\frac{f (x, θ^{'})}{f (x, θ)}$
is a function dependent only on $T (x)$ .

Barrett Osborn 2022-11-05

How to show mathematically max of uniform is a sufficient statistic?

pin1ta4r3k7b 2022-11-05

Let $X_{1}, \dots, X_{n}$ be iid from a uniform distribution $U [θ - \frac{1}{2}, θ + \frac{1}{2}]$ with $θ \in R$ unknown. Show that the statistic $T (X) = (X_{(1)}, X_{(n)})$ is minimal sufficient but not complete.

tramolatzqvg 2022-11-05

Let $X_{1}, X_{2}$ Poisson random variables with mean $μ$ . Is $T = X_{1} - X_{2}$ a sufficient statistic?

Madison Costa 2022-11-04

Why is the statistic $t = r \sqrt{\frac{n - 2}{1 - r^{2}}}$ $\approx t (n - 2)$ ?

T-Statistics can help you answer questions about the mean of a population given a sample. This is done by using equations to calculate if the mean of the population is significantly different from a specific value, or to compare two distinct samples to each other. T-Statistics can provide powerful insights and answers, and are a great tool for anyone who wants to analyze a sample to draw conclusions. With the help of a t-statistic, you can answer questions such as "is the average of this sample significantly different from this given value?". T-Statistics can provide helpful information and give you the tools necessary to make effective decisions.

Simplify T-Statistic Learning with Plainmath's Expert Tips and Real-World Examples