Geometry -concepts and properties for SSC CGL Tier-I Geometry is one of the most important topics of Quantitative Aptitude section of SSC CGL exam. It

Triangles

$\mathrm{△}=\text{Figure with three sides}$.  Study the following triangle: A,B,C to points. a, b, c to sides. x, y, z to angles.

Perimeter of triangle $=a+b+c$
Remember that, Sum of all the angles is always ${180}^{\circ }$
i.e. $x+y+z={180}^{\circ }$

Classification of Triangles

Basically there are three types of triangles excluding right angle triangle. Let me tell you how they vary from each other.

• Scalene Triangle
• Isosceles Triangle
• Equilateral Triangle

Scalene Triangle: No side of triangle is equal.
Isosceles Triangle: Two sides of triangle are equal.
Equilateral Triangle: All sides of triangle are equal.

$A={s(s-a)(s-b)(s-c)}^{1/2}$
where, $s=(a+b+c)/2$

Properties of external angles of Triangle:

1. Sum of all exterior angles is ${360}^{\circ }$
Study the following set of triangles and their exterior angles,

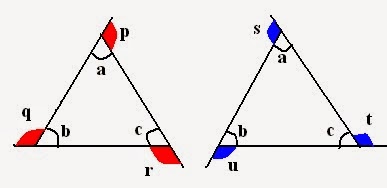
a, b, c to Interior angles. p, q, r and s, t, u to Exterior angles.
So, sum of exterior angles $={360}^{\circ }$ i.e. $p+q+r={360}^{\circ }$ and $s+t+u={360}^{\circ }$
2. Next property of exterior angle which is important in paper point of view:

External angle = Sum of two internal angles.

For example: In above figures,
$r=a+b$
$q=a+c$
$s=b+c$ and so on.

Right angle Triangle

Following triangle is a right angle triangle i.e. a triangle with one out of three ${90}^{\circ }$ angle.

Area of right angle triangle 

Area$=\frac{1}{2}\times$ Base times Perpendicular 

Example with Solution

 Example: In following figure, CE is perpendicular to AB, angle $ACE={20}^{\circ }$ and angle $ABD={50}^{\circ }$. Find angle BDA:

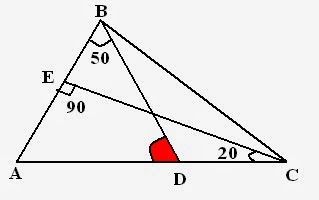
Solution: To Find: angle BDA
For this what we need --- angle BAD  Because, Sum of all angles $={180}^{\circ }$
Consider, triangle ECA,
$CEA+EAC+ACE={180}^{\circ }$ i.e. ${90}^{\circ }+{20}^{\circ }+EAC={180}^{\circ }$ Therefore, $EAC={70}^{\circ }$
Now, come to triangle ABD,
$ABD+BDA+BAD={180}^{\circ }$

${70}^{\circ }+{50}^{\circ }+BAD={180}^{\circ }$

Therefore, $BAD={60}^{\circ }$
Example: In given figure. BC is produced to D and angle $BAC={40}^{\circ }$ and angle $ABC={70}^{\circ }$. Find angle ACD:

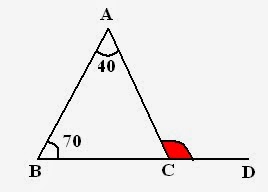
 Solution: In above figure, ACD is an exterior angle, and according to property, Exterior angle = Sum of interior angles Therefore, $ACD={70}^{\circ }+{40}^{\circ }={110}^{\circ }$
This is not the end of this chapter. These are just the basics. In next session, I will discuss some important results, properties (congruency, similarity) and much more. Always remember, Geometry needs practice and time.