Discoverand Master Vectors Solutions

Describe the vector space's zero vector (the additive identity).
${\displaystyle R^4}$

استخدم قاعدة السلسلة لإيجاد المشتقات الجزئية المشار إليها.

N = 

، p = u + vw ، q = v + uw ، r = w + uv ؛ 

و 

و 

    عندما u = 3 ، v = 5 ، w = 6

Suppose f is a differentiable function of x and y, and 

g(r, s) = f(2r − s, s2 − 7r).

 Use the table of values below to calculate 

gr(4, 3)

 and 

gs(4, 3).

Consider the following.

z = x2 + y2,   x = 5s + 6t,   y = s + t

Find 

 and 

 by using the chain rule. (Enter your answers in terms of s and t.)

=

52s+62t

=

62s+74t

Find 

 and 

 by first substituting the expressions for x and y to write z as a function of s and t. (Enter your answers in terms of s and t.)

=

=

Do your answers for 

 agree?

YesNo    

Do your answers for 

 agree?

YesNo    

Use the chain rule to find 

 and 

.

z = tan−1(x6 + y6),   x = s ln(t),   y = tes

=

=

(a)

Find the point at which the given lines intersect.

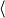
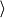
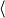
r	=	2, 3, 0	+	t 3, −3, 2
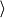
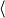
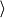
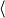
r	=	5, 0, 2	+	s −3, 3, 0

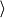
(x, y, z) = 

(b)

Find an equation of the plane that contains these lines.

Solve the system of equations

$\{\begin{array}{l}2x+3y=5\\ 5x-4y=2\end{array}$

The set $B=\{1+t^2,t+t^2,1+2t+t^2\}$ is a basis for ${\displaystyle {\mathbb{P}}_2}$. Find the coordinate vector of ${\displaystyle p\left(t\right)=1+4t+7t^2}$ relative to B.

(a) Find a nonzero vector orthogonal l to the plane the points P, Q, and R, and
(b) find the area of triangle PQR $P(1,0,1),Q(-2,1,3),R(4,2,5)$

Find the volume of the parallelepiped with adjacent edges PQ, PR, and PS. $P(3,0,1),Q(-1,2,5),R(5,1,-1),S(0,4,2)$

Use the cross product to find the sine of the angle between the vectors ${\displaystyle u=(2,3,-6)}$ and $v=(2,3,6)$.

Find ${\displaystyle \overrightarrow{a}+\overrightarrow{b},2\overrightarrow{a}+3\overrightarrow{b},\left|\overrightarrow{a}\right|}$ and $|\overrightarrow{a}-\overrightarrow{b}|$.
${\displaystyle \overrightarrow{a}=<5,-12>,\overrightarrow{b}=<-3,-6>}$

The work W done by a constant force F in moving an object from a point A in space to a point B in space is defined as $W=F\cdot \overrightarrow{AB}$. Find the work done by a force of 3 newtons acting in the direction ${\displaystyle 2i+j+2k}$ in moving an object 2 meters from ${\displaystyle (0,0,0)}$ to ${\displaystyle (0,2,0)}$.